Particle Tracking¶

Aim of the module¶

An advection-diffusion modelling tool for Lagrangian particles is proposed as a planning tool tuned to end-users and stakeholders. The particle tracking module (PARTRAC) allows to assess the dispersion of particles released in the Adriatic Sea (Fig. 14). Its outputs and derived variables can be customised and analysed based on the end-user requests and can be used to evaluate events as: impacts of aquaculture (larvae dispersion), tracking of floating debris and microplastic, point discharge and river plumes dispersion.

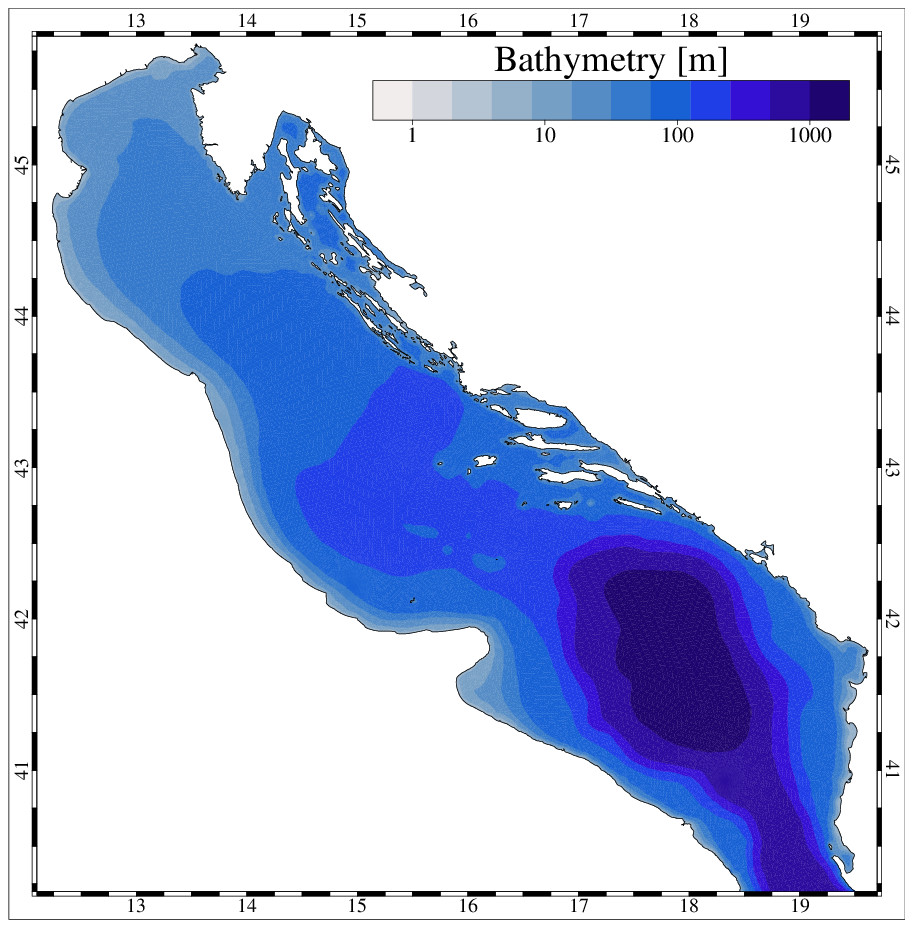
Fig. 14 Domain of the PARTRAC module.¶

The particle-tracking module simulates the trajectory of particles as a function of the hydrodynamic conditions simulated by the state of the art 3D SHYFEM oceanographic model.

The hydrodynamic SHYFEM model¶

SHYFEM solves the primitive equations, vertically integrated over each layer considering tidal, atmospheric and density-driven forces. SHYFEM is open source and freely available on the web pages http://www.ismar.cnr.it/shyfem and https://github.com/SHYFEM-model. SHYFEM has been already applied to simulate hydrodynamics in the Mediterranean Sea (Cucco et al. 2012; Ferrarin et al. 2013), in the Adriatic Sea (Bellafiore and Umgiesser 2010; Ferrarin et al. 2016, 2017, 2019), in several coastal systems (Umgiesser et al. 2014, and references therein).

The horizontal discretization of the state variables is carried out with the finite element method, with the subdivision of the numerical domain in triangles varying in form and size. Velocities are computed in the centre of the grid element, whereas the water levels are computed at the element vertices (nodes). Vertically the model applies Z layers with varying thickness. Most variables are computed in the center of each vertical layer, whereas stress terms and vertical velocities are solved at the interfaces between layers.

The model uses a semi-implicit algorithm for integration over time, which has the advantage of being unconditionally stable with respect to gravity waves, bottom friction and Coriolis terms, and allows transport variables to be solved explicitly. The Coriolis term and pressure gradient in the momentum equation, and the divergence terms in the continuity equation are treated semi-implicitly. Bottom friction and vertical eddy viscosity are treated fully implicitly for stability reasons, while the remaining terms (advective and horizontal diffusion terms in the momentum equation) are treated explicitly. A more detailed description of the model equations and of the discretization method is given in Umgiesser et al. (2004) and Ferrarin et al. (2017).

The lagrangian particle model¶

In SHYFEM a 3D lagrangian particle-tracking model coupled with the hydrodynamic code. The vertical components of the turbulent diffusion velocity is computed using the Milstein scheme (Gräwe and Wolff 2010). The horizontal diffusion was computed using a random walk technique based on Fisher et al. (1979), with the turbulent diffusion coefficients obtained by means of the Smagorinsky (1993) formulation. The off-line particle-tracking model uses the Eulerian hydrodynamic fields generated by the hydrodynamic model. The main advantage of the off-line approach is that the trajectory calculation typically takes much less computational effort than the driving hydrodynamic model.

The particle-tracking module of SHYFEM was successfully applied and validated by Cucco et al. (2012, 2016) and Quattrocchi et al. (2016) in the Sardinian coastal waters and by Ferrarin et al. (2019) in the Adriatic Sea.

SHYFEM model set-up in the Adriatic Sea¶

The numerical computation is performed on a spatial domain that represents the whole Adriatic Sea by means of the unstructured grid. To adequately resolve the river-sea continuum, the unstructured grid also includes the lower part of the other major rivers flowing into the Adriatic Sea. The use of elements of variable sizes, typical of finite element methods, is fully exploited, in order to suit the complicated geometry of the basin, the rapidly varying topographic features. The numerical grid of the Adriatic Sea consists in approximately 110,000 triangular elements with a resolution that varies from 5 km in the open-sea to few hundred meters along the coast (Fig. 15).

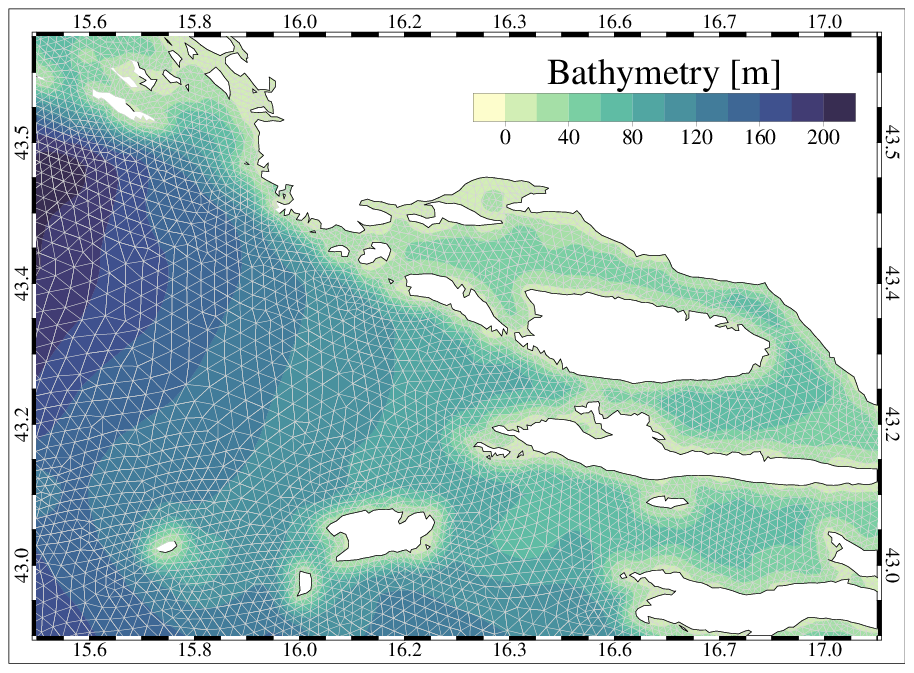
Fig. 15 Zoom of the unstructured grid near Split.¶

Because of the wide area, the bathymetry of the Adriatic was obtained by merging several datasets, having different spatial resolution and obtained using different measurement approaches, but the same reference datum (Genoa 1942 - IGM42). The resulting bathymetry, interpolated and superimposed on the triangular mesh, is shown above.

In this model application, the water column is discretized in 34 vertical layers with variable thickness ranging from 1m, in the topmost 10m, to 100m for the deepest layer of the Adriatic Sea. The vertical discretization of the surface layers allows one to describe the tidal propagation over the shallow tidal flats and the vertical structure of the tidal flow in the tidal channel network. The bottom drag coefficient is computed using a logarithmic formulation via bottom roughness length, set homogeneous over the whole system to a value of 0.01 m (Ferrarin et al. 2017).

The meteorological forcing is supplied by the MOLOCH limited-area, high-resolution model, developed and implemented at CNR-ISAC (National Research Council of Italy - Institute of Atmospheric Sciences and Climate) with a daily operational chain (http://www.isac.cnr.it/dinamica/projects/forecasts). The MOLOCH model is implemented with a horizontal grid spacing of 0.0113 degrees, equivalent to 1.25 km, and with 60 atmospheric levels and 7 soil levels. This model chain has already been successfully validated over the Adriatic Sea (Davolio et al. 2015, 2017). The atmospheric forcing fields are horizontally interpolated at each ocean grid node by means of a bilinear technique.

In order to improve representation of the coastal freshwater discharge, the lower part of major rivers are included in the unstructured numerical mesh. Daily river discharge values, derived from automatic hydrometric stations nearest to river mouths, are used for the rivers Isonzo, Aussa, Corno, Zellina, Cormor, Turgnano, Stella, Lemene, Livenza, Piave, Brenta-Bacchiglione-Gorzone, Adige, Po, Reno, Lamone, Fiumi Uniti, Savio, Uso, Marecchia, Metauro, Esino and Tronto. For the other rivers considered in this study (Tagliamento, Natissa, Canale dei Lovi, Sile, the tributaries of the Venice Lagoon, Po di Levante, Po di Volano, Fortore, Ofanto, Vijuse, Seman, Shkumbi, Erzen, Ishm, Mat, Bojana, Ombla, Neretva, Cetina, Krka, Zrmanja) discharges are prescribed using monthly or annual mean climatological values. Due to a lack of available observations, river inflow surface salinity is fixed to a constant value of 0.1 at the river boundaries.

The use of an unique numerical mesh for the whole Adriatic Sea limits the open sea boundaries to the Strait of Otranto at the southern end of the Adriatic Sea. Each node of the Otranto open boundary is treated by defining water level, current velocity, salinity and water temperature. The sea level and the current velocity conditions were obtained by summing the hourly tidal signal derived from the FES2012 global tidal model (Carrère et al. 2012) and the daily water level and baroclinic velocity predicted by the Mediterranean Forecast System (MFS, Tonani et al. 2008), available via the Copernicus Marine Environmental Monitoring Service (http://marine.copernicus.eu/). The total water levels are imposed to the boundary nodes, while the total current velocity are nudged using a relaxation time of 3600 s. Water temperature and salinity boundary conditions are computed using the oceanographic fields of MFS.

MFS 3D fields of sea temperature and salinity are nudged during the simulation. Nudging data are given for all nodes of the unstructured grid. The value of the relaxation coefficient is spatially varying over the model domain (as a function of the grid resolution) from 2 days in the open sea and increasing, thus diminishing the restoration contribution, toward the coast. Therefore, the nudging allows the model state to be reconciled with the assimilated MFS data in the open sea and to fully compute the hydrodynamics along the coast.

PARTRAC module inputs¶

PARTRAC is based on a case-study driven approach. A case-study is defined as pre-configured set of specific characteristic of the Adriatic Sea circulation and characteristics of the particles to be simulated. The user can easily select the deployment locations of the lagrangian particles by defining polygons through the web-based particle tracking interface (see as an example Fig. 16 representing a polygon defined along the Emilia-Romagna coast).

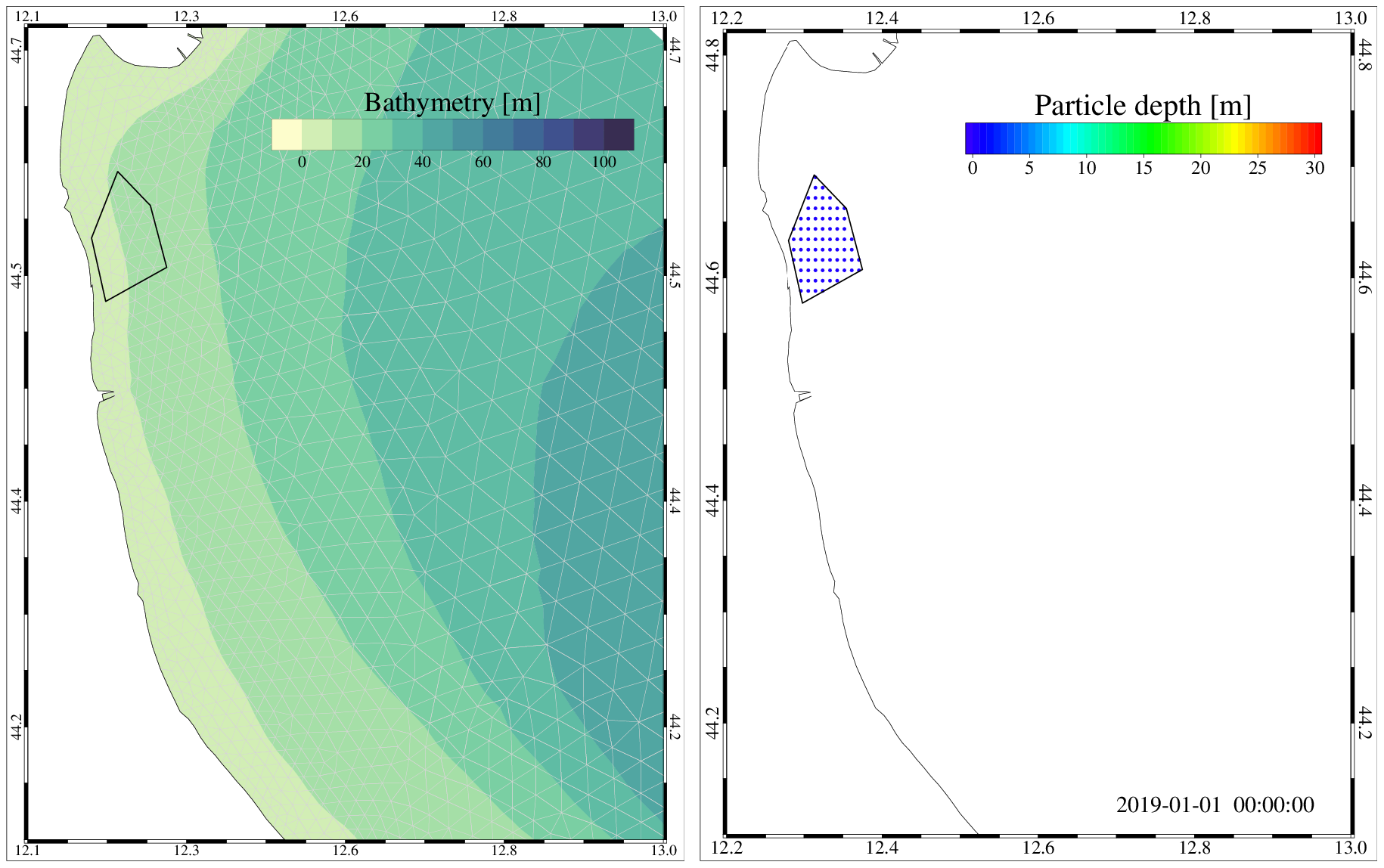
Fig. 16 Example of a polygon for particles deploiment (left) and initial particle distribution (right).¶

In the PARTRAC module, three sea condition scenarios are considered:

mean conditions obtained as a multi-year average;
winter conditions obtained as average over the winter months (December, January and February);
summer conditions obtained as average over the summer months (June, July, August).

The module could simulate particles released on the surface or through the whole water column.

The module allows to simulated the trajectories of the particles over a maximum period of 10 days.

The particles released by the lagrangian model can be customized by the user in terms of sinking velocity and decay rate. In this way, the user can simulate the dispersion of several substances. In Table 4 the customizable characteristics of the particles are described, together with example of the substances that can be considered.

Table 4 Customizable characteristics of the particles.¶
ID	Description	Sinking vel. [mm/s]	Decay rate [d-1]
1.1 1.2 1.3	General floating particle, e.g. larvae, floating litter	NONE	NONE
2.1 2.2 2.3	E.g. sediment [15 micron]	0.1	NONE
3.1 3.2 3.3	E.g. sediment [45 micron], microplastic [0.5 mm]	1.0	NONE
4.1 4.2 4.3	E.g. Sediment [150 micron], microplastic [2.5 mm]	10.0	NONE
5.1 5.2 5.3	E.g. Coliform bacteria [sea temperature 5 C]	NONE	0.1
6.1 6.2 6.3	E.g. Coliform bacteria [sea temperature 20 C, 20 m]	NONE	0.5
7.1 7.2 7.3	E.g. Coliform bacteria [sea temperature 20 C, 1 m]	NONE	1.0

ID X.1, X.2 and X.3 corresponds to mean, winter and summer sea conditions scenario, respectively. The settling velocity values [in mm/s] have been selected according to Soulsby (1997) for the sediments and Chubarenko et al. (2016) for the microplastics. The decay rate of coliform bacteria in seawaters were selected according to Eregno et al. (2018).

PARTRAC module outputs¶

The PARTRAC module produces outputs in terms of the positions of the released particles at daily time intervals. In this way, the user can follow the trajectories of the particles over the 10 days simulated period. Fig. 17 reports, as an example, the trajectories of the particles after 2 and 4 days from the release along the Emilia Romagna coast.

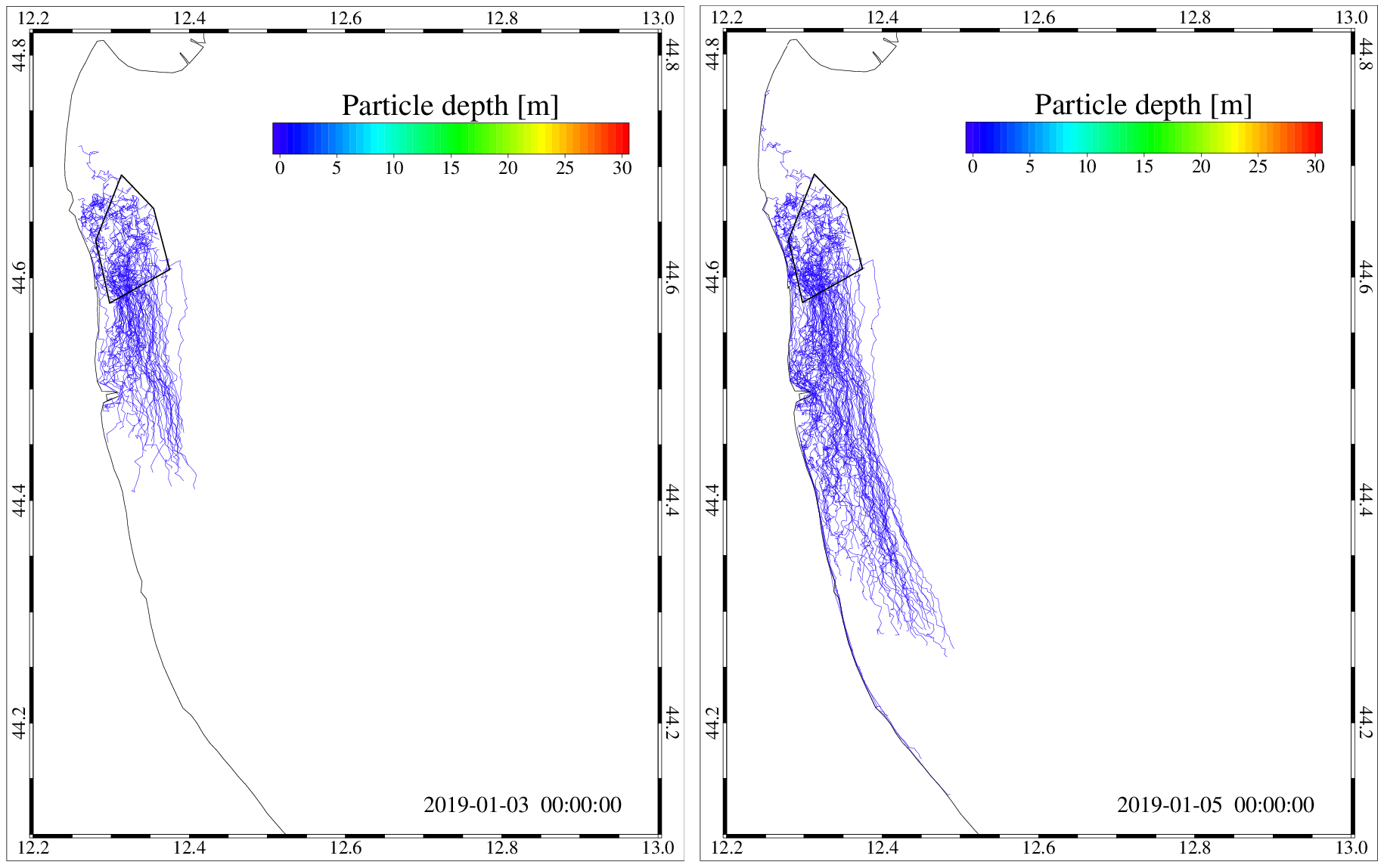
Fig. 17 Trajectories of surface particles after 2 and 4 days from the initial release.¶

Moreover, the module compute the particles concentration at daily frequency, computed on a regular grid of 500 m² (see as an example Fig. 18).

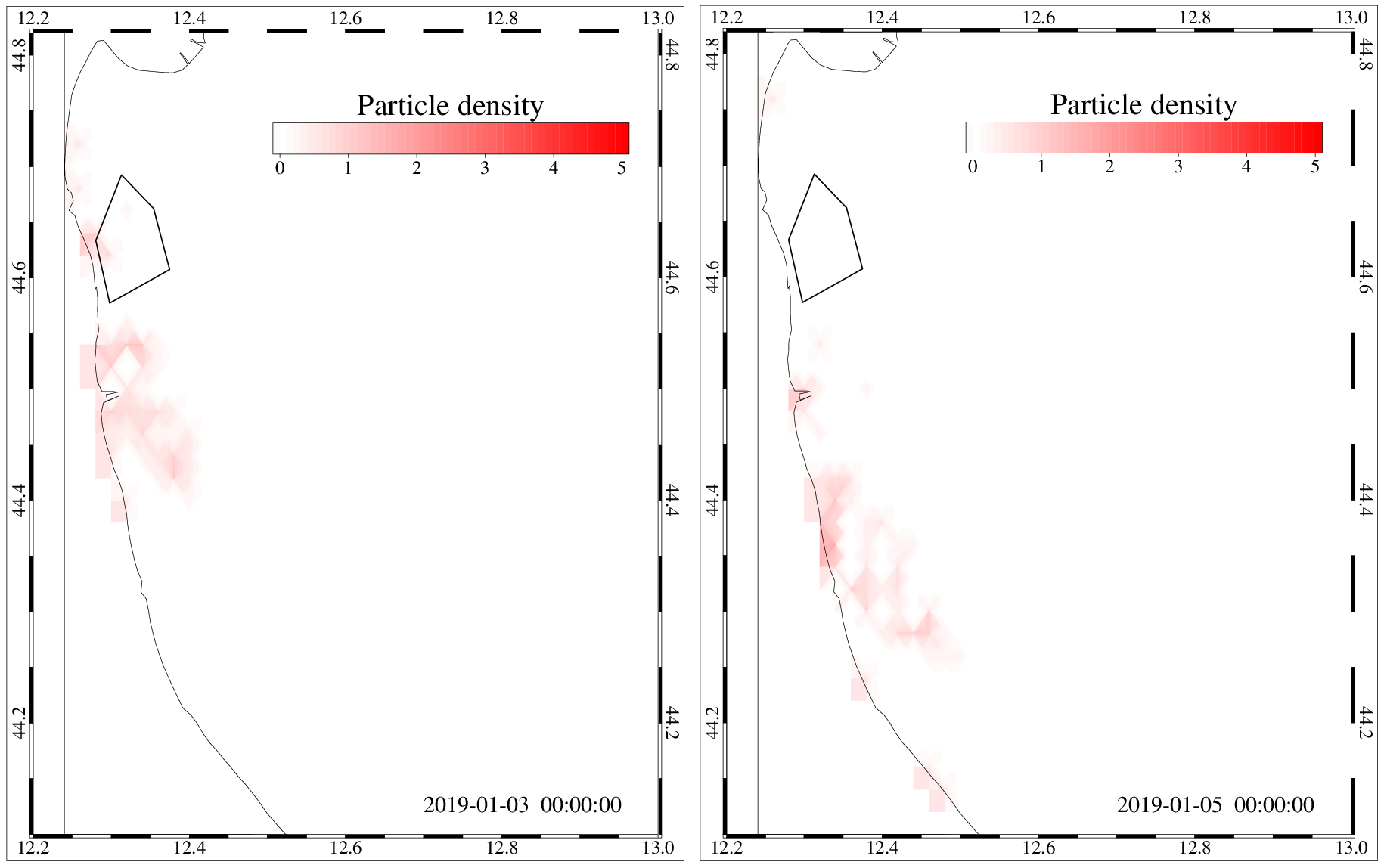
Fig. 18 Density of surface particles after 2 and 4 days from the initial release.¶

PARTRAC module authors¶

CNR-ISMAR staff: Christian Ferrarin, Michol Ghezzo, Stefano Menegon, Amedeo Fadini.

References¶

Bellafiore D, Umgiesser G. 2010. Hydrodynamic coastal processes in the North Adriatic investigated with a 3D finite element model. Ocean Dyn. 60:255-273.

Carrère L, Lyard F, Cancet M, Guillot A, Roblou L. 2012. FES2012: a new global tidal model taking advantage of nearly 20 years of altimetry. In: Ouwehand L, editor. Proceedings of 20 Years of Progress in Radar Altimetry Symposium. ESA SP-710.

Chubarenko, I., Bagaev, A., Zobkov, M., Esiukova, E., 2016. On some physical and dynamical properties of microplastic particles in marine environment. Mar. Pollut. Bull. 108,105-112.

Cucco A, Sinerchia M, Ribotti A, Olita A, Fazioli L, Perilli A, Sorgente B, Borghini M, Schroeder K, Sorgente R. 2012. A high-resolution real-time forecasting system for predicting the fate of oil spills in the Strait of Bonifacio (western Mediterranean Sea). Mar Pollut Bull. 64(6):1186-1200.

Cucco A, Quattrocchi G, Satta A, Antognarelli F, De Biasio F, Cadau E, Umgiesser G, Zecchetto S. 2016. Predictability of wind-induced sea surface transport in coastal areas. J Geophys Res Oceans. 121(8):5847-5871.

Davolio S, Henin R, Stocchi P, Buzzi A. 2017. Bora wind and heavy persistent precipitation: atmospheric water balance and role of air-sea fluxes over the Adriatic Sea. Q J R Meteorol Soc. 143(703):1165-1177.

Davolio S, Stocchi P, Benetazzo A, Bohm E, Riminucci F, Ravaioli M, Li XM, Carniel S. 2015. Exceptional Bora outbreak in winter 2012: validation and analysis of high-resolution atmospheric model simulations in the northern Adriatic area. Dynam Atmos Ocean. 71:1-20.

Eregno, F.E., Tryland, I., Myrmel, M., Wennberg, A., Oliinyk, A., Khatri, M., Heistad, A.,2018. Decay rate of virus and faecal indicator bacteria (FIB) in seawater and the concentration of FIBs in different wastewater systems. Microb. Risk Anal. 8,14e21.

Ferrarin C, Roland A, Bajo M, Umgiesser G, Cucco A, Davolio S, Buzzi A, Malguzzi P, Drofa O. 2013. Tide-surge-wave modelling and forecasting in the Mediterranean Sea with focus on the Italian coast. Ocean Model. 61:38-48.

Ferrarin C, Umgiesser G, Roland A, Bajo M, De Pascalis F, Ghezzo M, Scroccaro I. 2016. Sediment dynamics and budget in a microtidal lagoon - a numerical investigation. Mar Geol. 381:163-174.

Ferrarin C, Maicu F, Umgiesser G. 2017. The effect of lagoons on Adriatic Sea tidal dynamics. Ocean Model. 119:57-71.

Ferrarin C, Bellafiore D, Sannino G, Bajo M, Umgiesser G. 2018. Tidal dynamics in the inter-connected Mediterranean, Marmara, Black and Azov seas. Prog Oceanogr. 161:102-115.

Ferrarin, C., Davolio, S., Bellafiore, D., Ghezzo, M., Maicu, F., Mc Kiver, W., Drofa, O., Umgiesser, G., Bajo, M., De Pascalis, F., Malguzzi, P., Zaggia, L., Lorenzetti, G., 2019. Giorgia Manfé Cross-Scale Operational Oceanography in the Adriatic Sea Submitted Journal of Operational Oceanopraphy, 12, 86-103.

Fisher HB, List EJ, Koh RC, Imberger J, Brooks NH. 1979.Mixing in inland and coastal waters. San Diego, USA: Academic Press. 302 pp. (International Geophysics Series; vol. 66).

Gräwe U, Wolff JO. 2010. Suspended particulate matter dynamics in a particle framework. Environ Fluid Mech. 10 (1):21-39.

Quattrocchi G, Cucco A, Antognarelli F, Satta A, Maicu F, Ferrarin C, Umgiesser G. 2016. Optimal design of a lagrangian observing system for hydrodynamic surveys. J Oper Oceanogr. 9(sup1):s77-s88.

Soulsby, D., 1997. Dynamics of marine sands. Thomas Telford.

Smagorinsky J. 1993. Some historical remarks on the use of non-linear viscosities - 1.1 Introductory remarks. In: Galperin B, Orszag SA, editors. Large Eddy Simulation of Complex Engineering and Geophysical Flows, Proceedings of an International Workshop in Large Eddy Simulation. Cambridge, UK: Cambridge University Press; p. 1-32.

Tonani M, Pinardi N, Dobricic S, Pujol I, Fratianni C. 2008. A high-resolution free-surface model of the Mediterranean Sea. Ocean Sci. 4(1):1-14.

Umgiesser G, Ferrarin C, Cucco A, De Pascalis F, Bellafiore D, Ghezzo M, Bajo M. 2014. Comparative hydrodynamics of 10 Mediterranean lagoons by means of numerical modeling. J Geophys Res Oceans. 119(4):2212-2226.

Umgiesser G, Melaku Canu D, Cucco A, Solidoro C. 2004. A finite element model for the Venice Lagoon. Development, set up, calibration and validation. J Mar Syst. 51:123-145.